前言

设计BST二叉查找树，方便对二叉树进行结点的增删，采用双向不循环链表实现，每个结点
都需要2个指针，分别指向该结点的左子树（lchild）和右子树（rchild）
附加1：计算所有节点的数量
附加2: 计算所以叶子节点的数量（度为0）
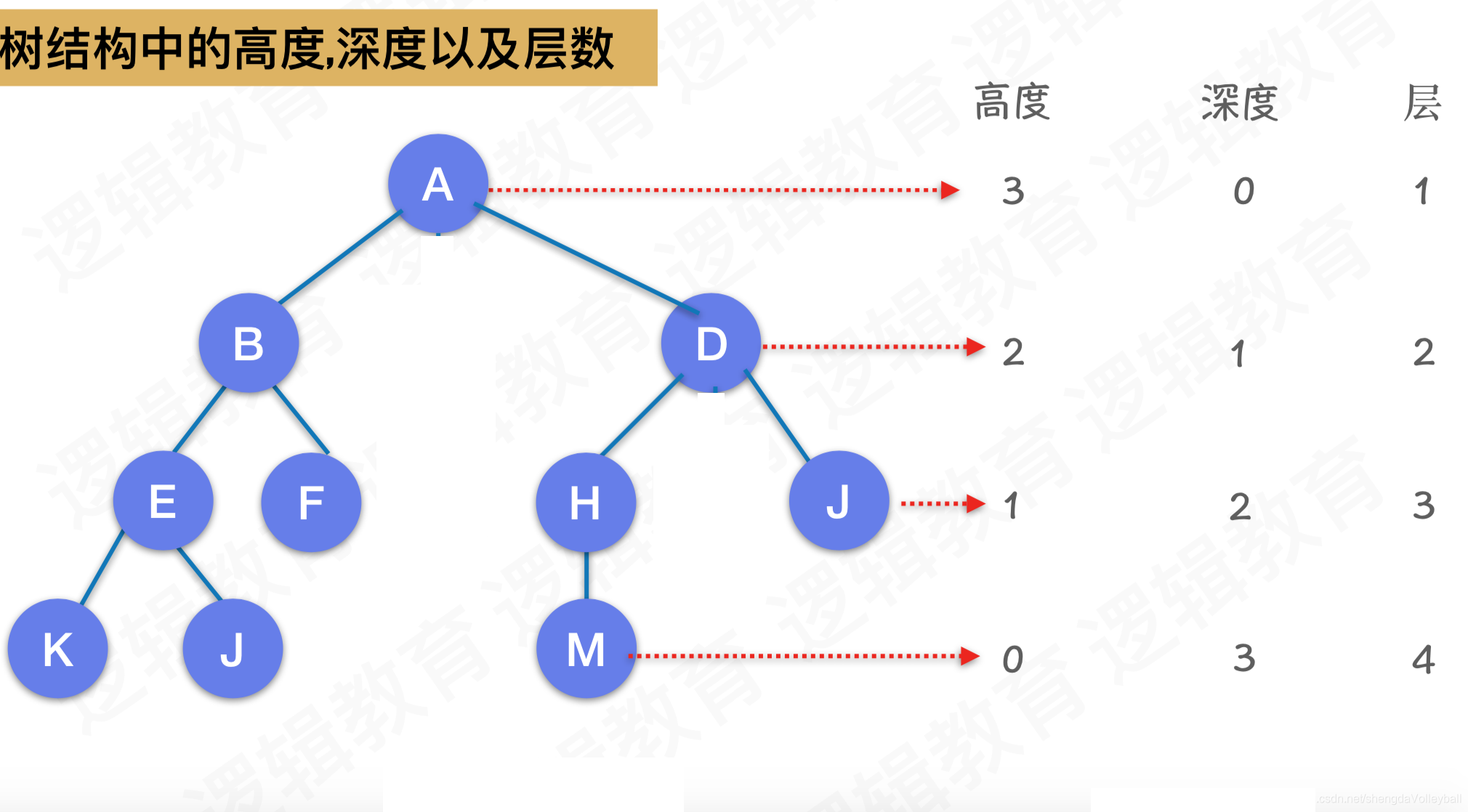
附加3: 计算二叉树的深度

二叉树

More info: BSTree

构造二叉树（BSTree）

构造BST树的结点 BST树中所以结点的数据类型应该是相同的（BSTreeNode）

1
2
3
4
5
6
7
//类型别名
typedef int dataType_t;
typedef struct BSTreeNode {
    dataType_t Keyval;                 //BST树的键值
    struct BSTreeNode *lchild;      //BST树的左子树的指针域
    struct BSTreeNode *rchild;      //BST树的右子树的指针域
} BSTNode_t;

创建一个带根结点的BST树，对BST树的根结点进行初始化（BSTree_Create）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
BSTNode_t* BSTree_Create(dataType_t Keyval)
{
    //1.1 创建一个根结点并给根结点申请内存
    BSTNode_t *Root = (BSTNode_t*)calloc(1,sizeof (BSTNode_t));
    if(Root == NULL)
    {
        perror("calloc memory for Root is Failed!\n");
        exit(-1);       //退出程序
    }

    //1.2 对根结点进行初始化
    Root->lchild = NULL;
    Root->Keyval = Keyval;
    Root->rchild = NULL;

    //1.3 把头结点地地址返回
    return Root;
}

创建新的结点，并对新结点进行初始化（数据域 指针域）（BSTree_NewNode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
BSTNode_t *BSTree_NewNode(dataType_t Keyval)
{
    //2.1 创建一个新结点并给新结点申请内存
    BSTNode_t *NewNode = (BSTNode_t *) calloc(1, sizeof(BSTNode_t));
    if(NewNode == NULL)
    {
        perror("calloc memory for NewNode is Failed!\n");
        return NULL;
    }

    //2.2 对新结点进行初始化（数据域 指针域2个）
    NewNode->lchild = NULL;
    NewNode->Keyval = Keyval;
    NewNode->rchild = NULL;

    //2.3 把新结点地地址返回
    return NewNode;
}

向BST树中加入结点 根结点的左子树键值比根结点的键值小，根结点的右子树键值比根结点的键值大 体现递归思想（BSTree_InsertNode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
bool BSTree_InsertNode(BSTNode_t *Root,dataType_t Keyval)
{
    //3.0 避免根结点地址丢失，对根结点地址进行备份
    BSTNode_t *Proot = Root;

    //3.1 创建新结点并对新结点进行初始化
    BSTNode_t *NewNode = BSTree_NewNode(Keyval);

    //3.2 此时分析当前BST树是否为空树（空树 or 非空树）
    //为空树
    if(Root == NULL)
    {
        //把新结点做为BST树的根结点
        Root = NewNode;
    }
    else  //为非空树,2种情况（键值 等于/不等于 根结点）
    {
        while(Proot)
        {
            //新结点的键值和当前新的根结点的键值比较,相等 直接退出
            if(NewNode->Keyval == Proot->Keyval)
            {
                printf("Can Not Insert,......\n");
                return false;
            }
            else  //新结点的键值和当前新的根结点的键值比较,不相等 继续分析
            {
                //新结点的键值和当前新的根结点的键值比较,小于 把根结点的左子树作为新的根
                if(NewNode->Keyval < Proot->Keyval)
                {
                    if(Proot->lchild == NULL)
                    {
                        Proot->lchild = NewNode;
                        break;
                    }
                    Proot = Proot->lchild;
                }
                else  //新结点的键值和当前新的根结点的键值比较,大于 把根结点的右子树作为新的根
                {
                    if(Proot->rchild == NULL)
                    {
                        Proot->rchild = NewNode;
                        break;
                    }
                    Proot = Proot->rchild;
                }
            }
        }
    }
    return true;
}

前序遍历 根左右 体现递归思想（BSTree_PreOrder）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool BSTree_PreOrder(BSTNode_t *Root)
{
    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return false;
    }
    
    //先输出根节点的键值
    printf("%d  \n",Root->Keyval);
    
    //在输出根节点的左子树
    BSTree_PreOrder(Root->lchild);
    //在输出根节点的右子树
    BSTree_PreOrder(Root->rchild);
}

中序遍历 左根右 体现递归思想（BSTree_InOrder）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool BSTree_InOrder(BSTNode_t *Root)
{
    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return false;
    }
    //先输出根节点的左子树
    BSTree_InOrder(Root->lchild);

    //在输出根节点的键值
    printf("%d  \n",Root->Keyval);

    //在输出根节点的右子树
    BSTree_InOrder(Root->rchild);
}

后序遍历 左右根 体现递归思想（BSTree_PostOrder）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool BSTree_PostOrder(BSTNode_t *Root)
{
    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return false;
    }
    //先输出根节点的左子树
    BSTree_PostOrder(Root->lchild);

    //在输出根节点的右子树
    BSTree_PostOrder(Root->rchild);

    //在输出根节点的键值
    printf("%d  \n",Root->Keyval);
}

附加1：计算所有节点的数量 可采用递归（BSTree_CountNode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int BSTree_CountNode(BSTNode_t *Root)
{
    int n1 = 0;     //记录左子树的节点数
    int n2 = 0;     //记录右子树的节点数

    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return 0;
    }

    //假设采用后序遍历计算节点数量
    n1 = BSTree_CountNode(Root->lchild);
    n2 = BSTree_CountNode(Root->rchild);

    return n1 + n2 +1;
}

附加2：计算所有叶子节点的数量 可采用递归（BSTree_CountLeafNode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int BSTree_CountLeafNode(BSTNode_t *Root)
{
    int n1 = 0;     //记录左子树的节点数
    int n2 = 0;     //记录右子树的节点数

    //使用递归函数，必须先写好终止条件
    if (Root == NULL)
    {
        return 0;
    }

    //说明只有一个根节点
    if(Root->lchild == NULL && Root->rchild == NULL)
    {
        return 1;
    }

    //说明有子树
    n1 = BSTree_CountLeafNode(Root->lchild);
    n2 = BSTree_CountLeafNode(Root->rchild);

    return n1 + n2;
}

附加3：计算二叉树的深度 可采用递归（BSTree_GetDepth）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int BSTree_GetDepth(BSTNode_t *Root)
{
    int n1 = 0;     //记录左子树的深度
    int n2 = 0;     //记录右子树的深度

    //使用递归函数，必须先写好终止条件
    if (Root == NULL)
    {
        return 0;
    }

//    //被下面情况包括
//    //说明只有一个根节点
//    if(Root->lchild == NULL && Root->rchild == NULL)
//    {
//        return 1;
//    }

    //说明有子树 计算左子树的深度 再 计算右子树的深度 最后 比较找最大再加一
    n1 = BSTree_GetDepth(Root->lchild);
    n2 = BSTree_GetDepth(Root->rchild);

    return ( (n1>n2)?n1:n2 ) + 1;
}

main主程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
int main()
{
    //1 创建一个带根节点的BST树
    BSTNode_t *Root = BSTree_Create(10);

    //2 向BST树插入新节点
    BSTree_InsertNode(Root,5);
    BSTree_InsertNode(Root,20);
    BSTree_InsertNode(Root,7);
    BSTree_InsertNode(Root,12);
    BSTree_InsertNode(Root,8);
    BSTree_InsertNode(Root,3);
    BSTree_InsertNode(Root,25);
    BSTree_InsertNode(Root,26);

//                     10
//            5                   20
//        3       7           12      25
//                    8                     26

    printf("前序遍历为:\n");
    BSTree_PreOrder(Root);

    printf("\n中序遍历为:\n");
    BSTree_InOrder(Root);

    printf("\n后序遍历为:\n");
    BSTree_PostOrder(Root);

    printf("\n总节点数：%d",BSTree_CountNode(Root));

    printf("\n所有叶子节点数：%d",BSTree_CountLeafNode(Root));

    printf("\n二叉树的深度：%d",BSTree_GetDepth(Root));
    
    return 0;
}

结果验证

1
2
3
4
5
6
7
8
9
10
11
前序遍历为:
10  5  3  7  8  20  12  25  26
中序遍历为:
3  5  7  8  10  12  20  25  26
后序遍历为:
3  8  7  5  12  26  25  20  10
总节点数：9
所有叶子节点数：4
二叉树的深度：4

进程已结束,退出代码0

汇总

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>

/*
设计BST二叉查找树，方便对二叉树进行节点的增删，采用双向不循环链表实现，每个节点
都需要2个指针，分别指向该节点的左子树（lchild）和右子树（rchild）
附加1：计算所有节点的数量
附加2: 计算所以叶子节点的数量（度为0）
附加3: 计算二叉树的深度
*/

//类型别名 节点有效键值
typedef int dataType_t;
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
//构造BST树的节点 BST树中所以节点的数据类型应该是相同的
typedef struct BSTreeNode {
    dataType_t Keyval;                 //BST树的键值
    struct BSTreeNode *lchild;      //BST树的左子树的指针域
    struct BSTreeNode *rchild;      //BST树的右子树的指针域
} BSTNode_t;
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
//1 创建一个带根节点的BST树，对BST树的根节点进行初始化
BSTNode_t* BSTree_Create(dataType_t Keyval)
{
    //1.1 创建一个根节点并给根节点申请内存
    BSTNode_t *Root = (BSTNode_t*)calloc(1,sizeof (BSTNode_t));
    if(Root == NULL)
    {
        perror("calloc memory for Root is Failed!\n");
        exit(-1);       //退出程序
    }

    //1.2 对根节点进行初始化
    Root->lchild = NULL;
    Root->Keyval = Keyval;
    Root->rchild = NULL;

    //1.3 把头节点地地址返回
    return Root;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
//2 创建新的节点，并对新节点进行初始化（数据域 指针域）
BSTNode_t *BSTree_NewNode(dataType_t Keyval)
{
    //2.1 创建一个新节点并给新节点申请内存
    BSTNode_t *NewNode = (BSTNode_t *) calloc(1, sizeof(BSTNode_t));
    if(NewNode == NULL)
    {
        perror("calloc memory for NewNode is Failed!\n");
        return NULL;
    }

    //2.2 对新节点进行初始化（数据域 指针域2个）
    NewNode->lchild = NULL;
    NewNode->Keyval = Keyval;
    NewNode->rchild = NULL;

    //2.3 把新节点地地址返回
    return NewNode;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
//3 向BST树中加入节点  根节点的左子树键值比根节点的键值小，根节点的右子树键值比根节点的键值大 体现递归思想
bool BSTree_InsertNode(BSTNode_t *Root,dataType_t Keyval)
{
    //3.0 避免根节点地址丢失，对根节点地址进行备份
    BSTNode_t *Proot = Root;

    //3.1 创建新节点并对新节点进行初始化
    BSTNode_t *NewNode = BSTree_NewNode(Keyval);

    //3.2 此时分析当前BST树是否为空树（空树 or 非空树）
    //为空树
    if(Root == NULL)
    {
        //把新节点做为BST树的根节点
        Root = NewNode;
    }
    else  //为非空树,2种情况（键值 等于/不等于 根节点）
    {
        while(Proot)
        {
            //新节点的键值和当前新的根节点的键值比较,相等 直接退出
            if(NewNode->Keyval == Proot->Keyval)
            {
                printf("Can Not Insert,......\n");
                return false;
            }
            else  //新节点的键值和当前新的根节点的键值比较,不相等 继续分析
            {
                //新节点的键值和当前新的根节点的键值比较,小于 把根节点的左子树作为新的根
                if(NewNode->Keyval < Proot->Keyval)
                {
                    if(Proot->lchild == NULL)
                    {
                        Proot->lchild = NewNode;
                        break;
                    }
                    Proot = Proot->lchild;
                }
                else  //新节点的键值和当前新的根节点的键值比较,大于 把根节点的右子树作为新的根
                {
                    if(Proot->rchild == NULL)
                    {
                        Proot->rchild = NewNode;
                        break;
                    }
                    Proot = Proot->rchild;
                }
            }
        }
    }
    return true;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
// 前序遍历 根左右 体现递归思想
bool BSTree_PreOrder(BSTNode_t *Root)
{
    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return false;
    }
    
    //先输出根节点的键值
    printf("%d  ",Root->Keyval);
    
    //在输出根节点的左子树
    BSTree_PreOrder(Root->lchild);
    //在输出根节点的右子树
    BSTree_PreOrder(Root->rchild);

    return true;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
// 中序遍历 左根右 体现递归思想
bool BSTree_InOrder(BSTNode_t *Root)
{
    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return false;
    }
    //先输出根节点的左子树
    BSTree_InOrder(Root->lchild);

    //在输出根节点的键值
    printf("%d  ",Root->Keyval);

    //在输出根节点的右子树
    BSTree_InOrder(Root->rchild);

    return true;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
// 后序遍历 左右根 体现递归思想
bool BSTree_PostOrder(BSTNode_t *Root)
{
    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return false;
    }
    //先输出根节点的左子树
    BSTree_PostOrder(Root->lchild);

    //在输出根节点的右子树
    BSTree_PostOrder(Root->rchild);

    //在输出根节点的键值
    printf("%d  ",Root->Keyval);

    return true;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
// 附加1：计算所有节点的数量 可采用递归
int BSTree_CountNode(BSTNode_t *Root)
{
    int n1 = 0;     //记录左子树的节点数
    int n2 = 0;     //记录右子树的节点数

    //使用递归函数，必须先写好终止条件
    if(Root == NULL)
    {
        return 0;
    }

    //假设采用后序遍历计算节点数量
    n1 = BSTree_CountNode(Root->lchild);
    n2 = BSTree_CountNode(Root->rchild);

    return n1 + n2 +1;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
// 附加2：计算所有叶子节点的数量 可采用递归
int BSTree_CountLeafNode(BSTNode_t *Root)
{
    int n1 = 0;     //记录左子树的节点数
    int n2 = 0;     //记录右子树的节点数

    //使用递归函数，必须先写好终止条件
    if (Root == NULL)
    {
        return 0;
    }

    //说明只有一个根节点
    if(Root->lchild == NULL && Root->rchild == NULL)
    {
        return 1;
    }

    //说明有子树
    n1 = BSTree_CountLeafNode(Root->lchild);
    n2 = BSTree_CountLeafNode(Root->rchild);

    return n1 + n2;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////
// 附加3：计算二叉树的深度 可采用递归
int BSTree_GetDepth(BSTNode_t *Root)
{
    int n1 = 0;     //记录左子树的深度
    int n2 = 0;     //记录右子树的深度

    //使用递归函数，必须先写好终止条件
    if (Root == NULL)
    {
        return 0;
    }

//    //被下面情况包括
//    //说明只有一个根节点
//    if(Root->lchild == NULL && Root->rchild == NULL)
//    {
//        return 1;
//    }

    //说明有子树 计算左子树的深度 再 计算右子树的深度 最后 比较找最大再加一
    n1 = BSTree_GetDepth(Root->lchild);
    n2 = BSTree_GetDepth(Root->rchild);

    return ( (n1>n2)?n1:n2 ) + 1;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////

int main()
{
    //1 创建一个带根节点的BST树
    BSTNode_t *Root = BSTree_Create(10);

    //2 向BST树插入新节点
    BSTree_InsertNode(Root,5);
    BSTree_InsertNode(Root,20);
    BSTree_InsertNode(Root,7);
    BSTree_InsertNode(Root,12);
    BSTree_InsertNode(Root,8);
    BSTree_InsertNode(Root,3);
    BSTree_InsertNode(Root,25);
    BSTree_InsertNode(Root,26);
    
//                     10
//            5                   20
//        3       7           12      25
//                    8                     26

    printf("前序遍历为:\n");
    BSTree_PreOrder(Root);

    printf("\n中序遍历为:\n");
    BSTree_InOrder(Root);

    printf("\n后序遍历为:\n");
    BSTree_PostOrder(Root);

    printf("\n总节点数：%d",BSTree_CountNode(Root));

    printf("\n所有叶子节点数：%d",BSTree_CountLeafNode(Root));

    printf("\n二叉树的深度：%d",BSTree_GetDepth(Root));
    
    return 0;
}